 Crystallographic Topology 101
Crystallographic Topology 101

Critical nets on orbifolds, as presented in Sect. 4., provide a wealth of local topology information about the parent space group and simple structures on that space group. The global topology information is also there, encoded in the macrodetails of the critical net graph and orbifold, but sometimes we need a more specific summary of the global picture. A simple example concerns the difference between face centered cubic (fcc) and hexagonal closest packing (hcp) which have identical substructures as indicated by the coordination vector. Lattice complexes are convenient for the next step up past the coordination vector. In fact, the fcc and hcp configurations have their own lattice complex symbols F and H, respectively.
Lattice Complex Background
Lattice complexes have a 77 year history in crystallography. We find much of the literature on lattice complexes more complex than we need for our application, but there is a well written paper, Hellner (1965), which describes the basics we use. Once those basics are understood, certain key tabulations in Fischer, Burzlaff, Hellner, and Donnay (1973); Koch (1984); and Fischer and Koch (1995) become useful. The definition given in the most recent reference is that a lattice complex is the set of all point configurations that may be generated within one type of Wyckoff set. Hellner's definition is that a lattice complex is an arrangement of equivalent points (or equipoints) that are related by space group symmetry operations, including lattice translations.
Lattice complexes are configurations of points that recur at least once but usually repeatedly throughout the family of all space groups. For example, the body-centered lattice complex, which is given the symbol "I", has symmetry equivalent points at 0,0,0 and 1/2,1/2,1/2 within the unit cell. This occurs in 38 space groups with orthorhombic or higher symmetry.
The "characteristic space-group type" of a lattice complex
is defined as the highest symmetry space group that can generate the
lattice complex. All other space groups with the same lattice complex
are subgroups of that characteristic space group, but not all the
subgroups contain the lattice complex (i.e., being a subgroup is a
necessary but not sufficient condition). For lattice complex I, the
characteristic space-group type is Im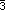 m; and the
"characteristic space-group site" is m
m; and the
"characteristic space-group site" is m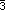 m at Wyckoff
position a in space group Im
m at Wyckoff
position a in space group Im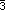 m, which is a
fixed point with zero degrees of freedom.
m, which is a
fixed point with zero degrees of freedom.
Point Configuration Complexes
Any lattice complex that has its characteristic space-group site on a fixed point is called an invariant lattice complex. Those with one degree of freedom are called univariant lattice complexes, etc. There are 25 invariant lattice complexes. Listed in order of the number of points [n] per cell in a lattice complex, they are: [1] P; [2] C, E, G, I; [3] J, N, +Q, R; [4] vD, F, +Y; [6] J*, W; [8] D, vT, +Y*; [9] M; [12] S, +V, W*; [16] T, Y**; [24] S*, V*. The lattice complex W* for example is called a twelve pointer. Those equivalent to Bravais lattices are P, C, I, R, and F.
Assigning all Wyckoff positions of all space groups to lattice complexes
produces a total of 402 lattice complexes which are tabulated in Fischer,
Burzlaff, Hellner, and Donnay (1973) and Fischer and Koch (1995). Our
main interest is point configurations rather than the general lattice
complexes as such. A lattice complex such as the invariant "I" can be a
subset of a univariant (or divariant) lattice complex. For example, the
Wyckoff position 16(c) of space group I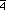 3d (#220)
produces "I" when the
variable x in x,x,x (i.e., on the body diagonal 3-fold axis) is set to
zero since in that space group there is no fixed point at 0,0,0. The same
Wyckoff position also has a Y** site at x = 1/8.
3d (#220)
produces "I" when the
variable x in x,x,x (i.e., on the body diagonal 3-fold axis) is set to
zero since in that space group there is no fixed point at 0,0,0. The same
Wyckoff position also has a Y** site at x = 1/8.
These subset special positions are not identified in the lattice complex tables and it necessary to consult tabulations such as Koch (1984) to find them. Unfortunately only the cubic space groups have been analyzed in this manner. See Koch and Fischer (1985) for additional details about this subject called the limiting complexes of lattice complexes. The tabulation of cubic point configurations by Koch (1984) lists the locations of all point positions with fewer than three degrees of freedom related to sphere packing and Dirichlet partitions within the cubic space group family as well. We use the Koch tabulation to identify lattice complex point sites along orbifold axes and on mirrors.
Dirichlet partitioning of 3-space around a point lattice complex site is carried out by placing planes normal to vectors between neighboring points of the complex at midpoints of the vectors. This forms a convex polyhedron around the origin site point in which all points within the polyhedron are closer to the origin site point than to any other site of the complex. The vertices of a Dirichlet polyhedron are sometimes called interstices, implying holes between spherical atoms.
For the invariant lattice complex P, which represents simple cubic packing, the center, face, edge, and vertex barycenters (centroids) fall on the peak, pass, pale, and pit critical points of the critical net, respectively, as expected. For the body-centered lattice complex I, this correlation does not hold since the bcc peaks, passes, pales, and pits are on the center, 8 hexagonal faces, 24 vertices, and 6 square faces, respectively, rather than on the 14 faces, 36 edges, and 24 vertices of the bcc truncated octahedron Dirichlet polyhedron.
Because of such discrepancies, we recommend that critical nets be used in place of Dirichlet polyhedra tiling when practical. The Dirichlet partitioning algorithm is not based on crystallographic topology principles. Thus the bcc rhombohedral dodecahedron coordination polyhedron (12 faces, 24 edges, 14 vertices) is not dual to the bcc truncated octahedron Dirichlet polyhedron (Loeb,1970), and it serves as a classic counterexample to the postulated duality.
By using critical nets corresponding to more complex crystal structures, we would be able to specify, utilize, and label many more lattice complex sites than we do with the very simple structures we are currently using. Such critical net graphs could be huge and impossible to draw, but that is a very promising area for future computational topology research. We have some tentative plans for using matroids (Björner, 1993) in research of this nature and may do something along that line in some collaborative research which utilizes macromolecular critical nets. We first got involved in crystallographic topology by using critical point analysis on protein electron density maps in the 1970s. In that project, we wrote the ORCRIT computer program, which, after sitting on the shelf for 15 years, is now being used productively by our Queen's University colleagues (Leherte, 1994).
Lattice Complex Splitting Equations
The lattice complexes we need in the next few example are P, I, F, T, D, J*, and W* denoting primitive, body-centered, face-centered, tetrahedral, diamond, jack-shaped (from the "pick up jacks" children's game), and non-intersecting (German: windschief), respectively. Symbols with a 2 subscript (e.g., P2) indicate doubling in all three directions to give 8 times as many points. A superscript number denotes the degree of positional freedom at that site.
The lattice-complex splitting equations for the cubic lattice complexes interrelate these lattice complexes. Shown pictorially in Hellner (1965), these include I=P+P", P2=F+F", P2=D+D", P2=I+J*, J*=J+J^, W*=W+W^, and F=P+J, with " denoting translation along a body diagonal by (1/2,1/2,1/2) and ^ denoting translation along a cell edge such as (1/2,0,0). In our orbifold application, these equations will appear as graphs with a translation of (1/2,1/2,1/2) appearing as a region along a 3-fold axis, and (1/2,0,0) as a region along an even-order axis.
Lattice Complexes in Critical Nets on Orbifolds: Examples
The body-centered cubic family of Fig. 4.3 provides our first example of a lattice complex family. The face-centered cubic and the diamond families are shown in Figs. 5.1 and 5.2, respectively. Other examples are shown in Sect. 6.
Notes on all orbifold figures:
Notes on Fig. 5.1:
Notes on Fig 5.2:
Comparative Topology of Critical Nets on Orbifolds
An interesting feature of critical nets is duality in which the
critical point set's peaks, passes, pales, and pits can be relabeled in
inverse order to produce a dual critical net. We note that the
diamond structure critical nets shown in Fig. 5.2 are self dual in
that there are internal symmetries relating the top and bottom halves
of the critical nets. The face-centered cubic critical nets in Fig.
5.1 and the body-centered cubic critical nets in
Fig. 4.3 are not self
dual; consequently we can turn those critical nets upside down to
produce different families of critical nets.
The diamond critical net is so named because gemstone diamond has that
structure. The diamond's three-dimensional tetrahedral carbon
structure shown in
Fig. 3.1
has its only atom of the asymmetric unit
at the peak site of space group Fd
The comparative crystallographic topology of these three carbon-crystal
critical nets is informative since graphite is the topological dual of
hexagonal diamond. In addition, both have the same symmetric summed
critical net vector as regular cubic diamond, as demonstrated in Fig. 5.3.
Fig. 5.3 also shows the critical net for hexagonal closest packing
(hcp) for comparison with that of face centered cubic (fcc) in Fig. 5.2
which, as we previously mentioned, has the same local topology as hcp.
Graphite, hexagonal diamond, and hcp all crystallize in the same
hexagonal space group, P63/mmc. The Wyckoff set and
orbifold for that space group also are shown in Fig. 5.3.
In Fig. 5.3, the nodes of the critical net graphs contain the
appropriate Wyckoff symbol rather than the lattice complex, but the
Wyckoff to lattice complex mapping is a,b->Pc; c,d->E; and g->N, where
Pc stands for primitive with doubling along c.
The upper left drawing of Fig. 5.3 has a single 2' axis, h, extending
around the upper edge of the kitchen measuring-scoop shaped basin.
There are three 3'-axis intersections (b, c, & d) that h traverses
to form a complete loop. The leading end of the scoop has a single
3'-axis half-loop, f, while the support spine along the back of the
scoop is a second 3' axis, e. The bottom point, a, at the spine, e,
gives rise to a 2 axis that goes through open space from point a to
point c in the forward end of the scoop. Everything below the
2' axis, h, is covered by mirror floor, k, while that above h has a
mirror ceiling, j.
The hcp critical net in the upper right has the multiplicities shown
for each critical net component and the coordination vector
(8)(12;2;4;3;2;8,4)(6,1), which is identical to that for fcc in Fig.
5.1. The summed hcp multiplicities are all smaller than those for fcc
by a factor of two because of the supercell in fcc caused by repeating
after three layers in fcc versus two layers in hcp.
Duality Example
The bottom two critical-net drawings compare the duality of graphite
and hexagonal diamond. Note that the coordination vector
(4)(4,2,6,6,2,4)(4) is identical to that for diamond in Fig. 5.2 while
the summed multiplicity vector (16)(4,16,8,48,8,16,4)(16) is half that
of diamond, which again tells us there are more layers in real diamond
but the averaged local topology is identical.
How can the physical properties of the various carbon crystal
structures be so different when they have the same local topology? The
answer is basically that topology has little connection with chemistry
in that a pass may or may not be a strong (e.g., covalent) bond. In
diamond and hexagonal diamond, all the passes correspond to covalent
bonds while for graphite there are no covalent bonds between layers.
Consequently, there is often as much topological detail between
chemical entities as there is within them as shown in the graphite
example.
The x and z values given under each critical net in Fig. 5.3 provide
the variable position parameters for occupied univariate and divariate
Wyckoff sites. Note that we felt it necessary to make some slight
adjustment in going from graphite to hexagonal diamond based on
empirical eyeballing of the ORTEP diagrams in trying to keep pass and
pale configurations as planar as possible. We have not done any
analytical positioning of critical points based on the Gaussian density
Morse function calculations since for most simple examples studied to
date, the space groups usually provide enough fixed points to predefine
the critical net details fairly well. That will not be the case for
more complex crystal structure problems.
A crystallographic peculiarity of space group P63/mmc
should be noted.
If the signs of all z axis variables are changed, the c and d sites also
interchange. The reason is that c and d are the only two
fixed sites not on the vertical plane of symmetry in the orbifold of
Fig. 5.3. For that reason it took us a while to recognize the duality
since we solved the critical nets for the two structures independently
based on published atomic position parameters. We had not expected to
find non-trivial critical set duality in real structures so early in the
game; thus it may be a common phenomenon with exciting predictive
possibilities. The NaCl <---> primitive cubic situation shown in
Fig. 6.2)
might be termed a trivial duality since a primitive cubic structure with
two pits would at best be transitory and probably the result of some
lattice dynamic vibrational phenomenon.
Page last revised: July 2, 1996
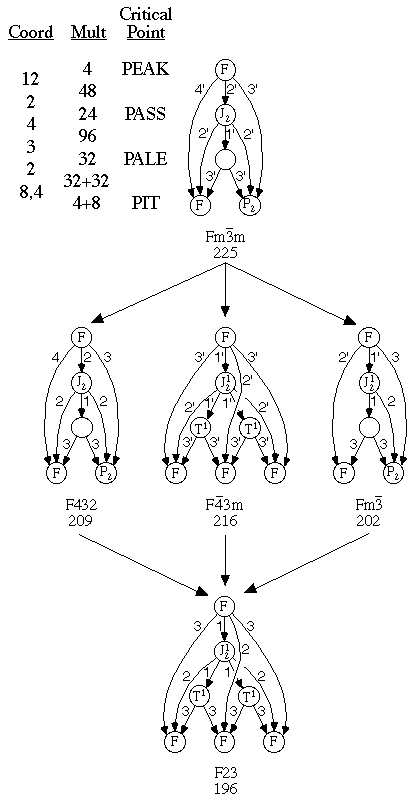
Figure 5.1. Face-Centered Cubic Critical Net Superimposed
onto Cubic Space Group Orbifolds.
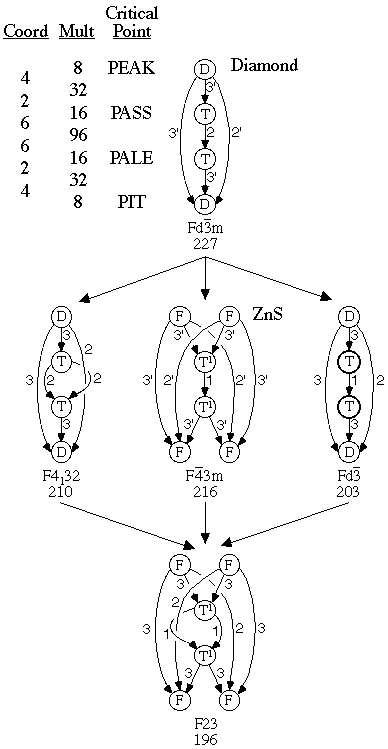
Figure 5.2. Diamond and ZnS Critical Nets Superimposed
onto Cubic Space Group Orbifolds.
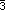 m.
Diamond is well known for its
hardness since the corner of a diamond crystal can scratch almost all
other solid materials. The graphite structure of
Fig. 3.2
is also
pure carbon but is a layered structure with such weak noncovalent
bonding between layers that it is commonly used as the writing "lead"
in pencils. Another form of crystalline carbon, hexagonal diamond
(shown in
Fig. 3.3)
also has three dimensional strong covalent bonding
but is a laboratory and mineral oddity not commonly available.
m.
Diamond is well known for its
hardness since the corner of a diamond crystal can scratch almost all
other solid materials. The graphite structure of
Fig. 3.2
is also
pure carbon but is a layered structure with such weak noncovalent
bonding between layers that it is commonly used as the writing "lead"
in pencils. Another form of crystalline carbon, hexagonal diamond
(shown in
Fig. 3.3)
also has three dimensional strong covalent bonding
but is a laboratory and mineral oddity not commonly available. 
Figure 5.3. Three Different Critical Nets on the Hexagonal Space Group
P63/mmc Orbifold.
 6. Cubic Space Group/Subgroup Families
6. Cubic Space Group/Subgroup Families
 Crystallographic Topology Home Page
Crystallographic Topology Home Page