 Crystallographic Topology 101
Crystallographic Topology 101

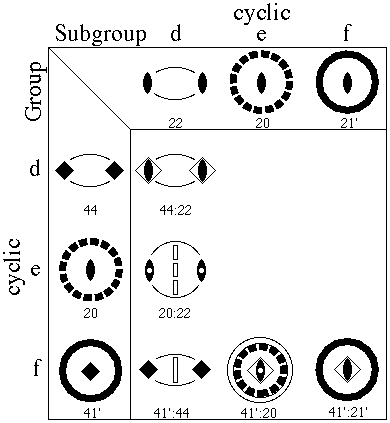
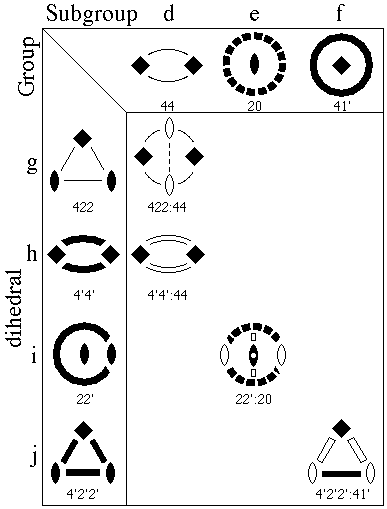
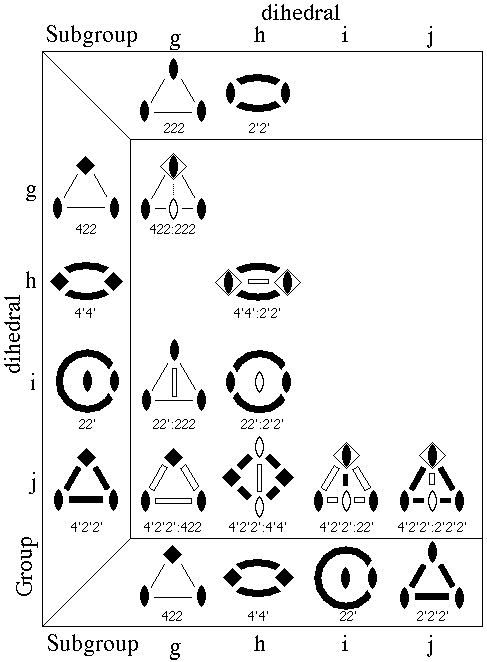
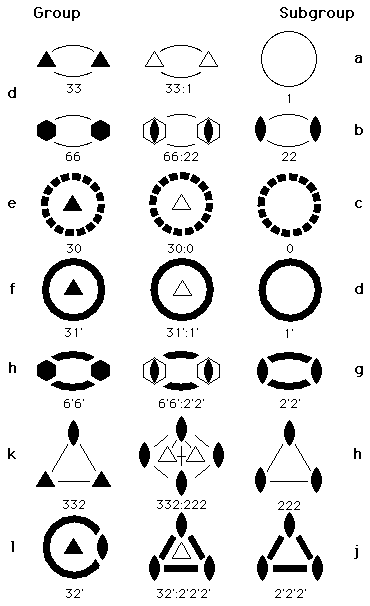
Figs. B.1, B.2, and B.3 illustrate 17 examples for the 15 families of bicolor elliptic 2-orbifolds, based on the 7 topology families belonging to the cyclic (d,e,f) and dihedral (g,h,i,j) point groups. Each member of the bicolor point group represents a group/normal-subgroup (G/H) pair of regular point groups, with the regular orbifold arising from the point group G.
One group representation from the orthorhombic-tetrahedral cluster (i.e., from the bottom layer of Fig. A.2) is shown on the left of Figs. B.1-B.3, and one to three regular orbifolds (H), from corresponding subgroups, on the top or bottom of the figures. The bicolor orbifold within the table is labeled G:H and has both black (symmetry) and white (antisymmetry) components. The H suborbifold is seen by ignoring the white (i.e., outlined) orbifold elements, and the G orbifold is seen by considering all elements to be equally valid.
The simplest examples are [hd] 4'4':44 in Fig. B.2 and [jg] 4'2'2':422 in Fig. B.3 for which only the mirrors have antisymmetry. Next in complexity are [dd] 44:22 and [ff] 41':21' in Fig. B.1 where a 90o rotation has antisymmetry, but the second order 180o has regular symmetry. This also occurs with [hh] 4'4':2'2' of Fig. B.3 except that in this case the angle between the mirrors reduces from 90o to 45o, and you simply have to ignore one of the original outside mirror symbols. Similarly, with [gg] 422:222 of Fig. B.3 where a new 2-fold axis becomes active, we ignore one of the original black 2-folds.
In practice, we do not simply "ignore" the doubled symbols since the chief application is analyzing the changes in the singular set in pairs of Euclidean 3-orbifolds. The doubling of the orbifold symbol accompanies a doubling of the original fundamental domain in the group to subgroup transformation.
The most complex symbols involve the projective plane [fe] 41':20 in Fig. B.1 and [ie] 22':20 in Fig. B.2, but the detailed symbolism can be deduced from the triads of symbols.
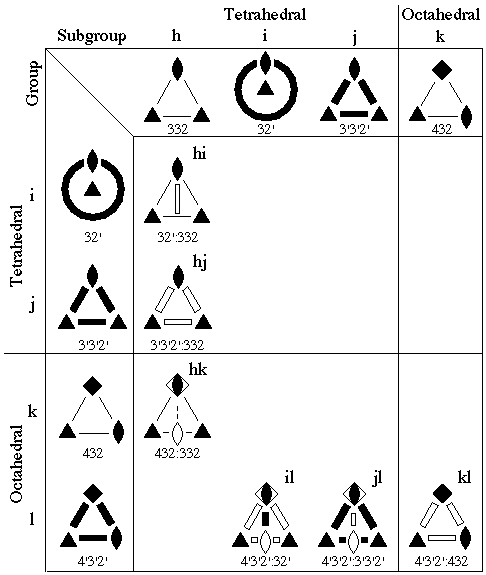
Related diagrams for the cubic bicolor elliptic 2-orbifolds and the tricolor elliptic 2-orbifolds are shown in Figs. B.4 and B.5, respectively.
 Appendix A. Subgroup Families from Color Groups
Appendix A. Subgroup Families from Color Groups
 Crystallographic Topology Home Page
Crystallographic Topology Home Page
Page last revised: May 8, 1996